hudkubzel-05-06-037-c
$
\newcommand\tg{\operatorname{tg}}
\newcommand\cotg{\operatorname{cotg}}
\newcommand{\uhel}{{<}\kern-0.5em)\,}
\newcommand\abs[1]{\left| #1 \right|}
\newcommand\zav[1]{\left( #1 \right)}
\newcommand\zavhra[1]{\left[ #1 \right]}
\newcommand\zavslo[1]{\left\{ #1 \right\}}
\newcommand\zavlom[1]{\left< #1 \, \right>}
\newcommand{\podtrzeni}[1]{\underline{ #1 }}
\newcommand{\vysledek}[1]{\underline{\underline{#1}}}
\newcommand{\priume}[4]{
\Bigg\uparrow
\underline{
\begin{array}{rp{2.3cm}r}
#1 & \dots\dots\dots\dots\dots & #2 \\
#3 & \dots\dots\dots\dots\dots & #4
\end{array}}
\Bigg\uparrow}
\newcommand{\nepriume}[4]{
\Bigg\downarrow
\underline{
\begin{array}{rp{2.3cm}r}
#1 & \dots\dots\dots\dots\dots & #2 \\
#3 & \dots\dots\dots\dots\dots & #4
\end{array}}
\Bigg\uparrow}
\newcommand{\nepriumevpravo}[4]{
\Bigg\uparrow
\underline{
\begin{array}{rp{2.3cm}r}
#1 & \dots\dots\dots\dots\dots & #2 \\
#3 & \dots\dots\dots\dots\dots & #4
\end{array}}
\Bigg\downarrow}
$
$\textbf{Hudcová a Kubičíková 5.37 c) / s. 99}$
Štítky: kuželosečky, vyšetřování kuželoseček, parabola
Načrtněte graf funkce dané rovnicí $y=x^2-4$.
$\textbf{Řešení}$ $$y=x^2-4$$ Vyšetřit kuželosečku znamená rozhodnout, o jakou se jedná, a určit všechny její charakteristické vlastnosti.
V našem případě se jedná o parabolu, neboť jedna proměnná ($x$) je ve druhé mocnině a druhá proměnná ($y$) je v první mocnině.
Osa paraboly je rovnoběžná s tou osou, jejíž proměnná je v první mocnině. $$\vysledek{o \parallel o_y}$$
$\textbf{Souřadnice vrcholu paraboly}$
Nalezením nulového bodu výrazu $x$ získáme $x$-souřadnici vrcholu paraboly $V\zavhra{x;\,y}$ \begin{align*} x&=0 \end{align*} $y$ souřadnici vrcholu paraboly vypočítáme dosazením za $x=0$ \begin{align*} y &= x^2-4\\ y &= 0^2-4\\ y &= -4 \end{align*} $$\vysledek{\text{Souřadnice vrcholu paraboly}~\dots~V\zavhra{0;\,-4}}$$
Koeficient $a$ v zadané rovnici paraboly $y=x^2-4$ je roven $a=1$
$a > 0$ ... parabola je otevřená "nahoru"
$\textbf{Průsečíky paraboly $p$ s osami}$
Průsečík s $o_x$ ... $p \cap o_x$ ... $y=0$ \begin{align*} 0 &= x^2-4\\ x^2 &= 4\\ \abs{x} &= 2\\ x_1 &=-2\\ x_2 &=2 \end{align*} $$\vysledek{\text{Průsečíky}~p \cap o_x~\text{jsou dva}~\dots~\zavhra{-2;\,0}~\text{a}~\zavhra{2;\,0}}$$
Průsečík s $o_y$ ... $p \cap o_y$ ... $x=0$ \begin{align*} y&=x^2-4\\ y&=0^2-4\\ y&=-4 \end{align*} $$\vysledek{\text{Průsečík}~p \cap o_y = \zavhra{0;\,-4}}$$
$\textbf{Graf paraboly $p$}$
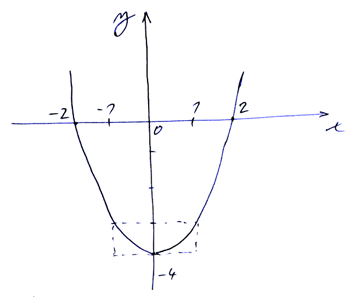
$\textbf{Konec příkladu}$
Štítky: kuželosečky, vyšetřování kuželoseček, parabola
Načrtněte graf funkce dané rovnicí $y=x^2-4$.
$\textbf{Řešení}$ $$y=x^2-4$$ Vyšetřit kuželosečku znamená rozhodnout, o jakou se jedná, a určit všechny její charakteristické vlastnosti.
V našem případě se jedná o parabolu, neboť jedna proměnná ($x$) je ve druhé mocnině a druhá proměnná ($y$) je v první mocnině.
Osa paraboly je rovnoběžná s tou osou, jejíž proměnná je v první mocnině. $$\vysledek{o \parallel o_y}$$
$\textbf{Souřadnice vrcholu paraboly}$
Nalezením nulového bodu výrazu $x$ získáme $x$-souřadnici vrcholu paraboly $V\zavhra{x;\,y}$ \begin{align*} x&=0 \end{align*} $y$ souřadnici vrcholu paraboly vypočítáme dosazením za $x=0$ \begin{align*} y &= x^2-4\\ y &= 0^2-4\\ y &= -4 \end{align*} $$\vysledek{\text{Souřadnice vrcholu paraboly}~\dots~V\zavhra{0;\,-4}}$$
Koeficient $a$ v zadané rovnici paraboly $y=x^2-4$ je roven $a=1$
$a > 0$ ... parabola je otevřená "nahoru"
$\textbf{Průsečíky paraboly $p$ s osami}$
Průsečík s $o_x$ ... $p \cap o_x$ ... $y=0$ \begin{align*} 0 &= x^2-4\\ x^2 &= 4\\ \abs{x} &= 2\\ x_1 &=-2\\ x_2 &=2 \end{align*} $$\vysledek{\text{Průsečíky}~p \cap o_x~\text{jsou dva}~\dots~\zavhra{-2;\,0}~\text{a}~\zavhra{2;\,0}}$$
Průsečík s $o_y$ ... $p \cap o_y$ ... $x=0$ \begin{align*} y&=x^2-4\\ y&=0^2-4\\ y&=-4 \end{align*} $$\vysledek{\text{Průsečík}~p \cap o_y = \zavhra{0;\,-4}}$$
$\textbf{Graf paraboly $p$}$

$\textbf{Konec příkladu}$