petakova-06-19-108-a
$
\newcommand\tg{\operatorname{tg}}
\newcommand\cotg{\operatorname{cotg}}
\newcommand{\uhel}{{<}\kern-0.5em)\,}
\newcommand\abs[1]{\left| #1 \right|}
\newcommand\zav[1]{\left( #1 \right)}
\newcommand\zavhra[1]{\left[ #1 \right]}
\newcommand\zavslo[1]{\left\{ #1 \right\}}
\newcommand\zavlom[1]{\left< #1 \, \right>}
\newcommand{\podtrzeni}[1]{\underline{ #1 }}
\newcommand{\vysledek}[1]{\underline{\underline{#1}}}
\newcommand{\priume}[4]{
\Bigg\uparrow
\underline{
\begin{array}{rp{2.3cm}r}
#1 & \dots\dots\dots\dots\dots & #2 \\
#3 & \dots\dots\dots\dots\dots & #4
\end{array}}
\Bigg\uparrow}
\newcommand{\nepriume}[4]{
\Bigg\downarrow
\underline{
\begin{array}{rp{2.3cm}r}
#1 & \dots\dots\dots\dots\dots & #2 \\
#3 & \dots\dots\dots\dots\dots & #4
\end{array}}
\Bigg\uparrow}
\newcommand{\nepriumevpravo}[4]{
\Bigg\uparrow
\underline{
\begin{array}{rp{2.3cm}r}
#1 & \dots\dots\dots\dots\dots & #2 \\
#3 & \dots\dots\dots\dots\dots & #4
\end{array}}
\Bigg\downarrow}
$
$\textbf{Petáková 6.19 108 a) / s. 51}$
Štítky: funkce, goniometrické funkce, trigoniometrie, mnohoúhelníky, výpočty
Strana pravidelného devítiúhelníku je $a=5\,\text{cm}$. Vypočítejte poloměr kružnice, kterou lze danému devítiúhelníku opsat.
$ \textbf{Řešení} $
Poloměrem $r$ kružnice opsané pravidelnému devítiúhelníku ABCDEFGHI je délka ramene rovnoramenného trojúhelníku $ABS$, viz následující obrázek.
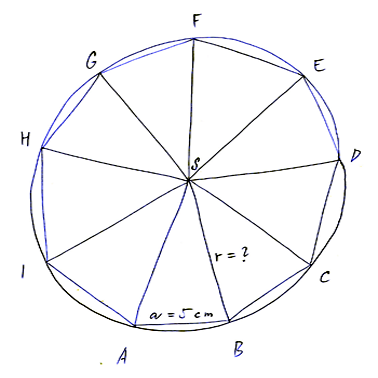
Velikost úhlu $ASB$ v pravidelném devítiúhelníku je rovna devítině plného úhlu ($360^\circ$) a vypočteme ji $$ \abs{\uhel ASB}=360^\circ : 9 = 40^\circ $$ Velikost poloměru $r$ vypočteme pomocí pravoúhlého trojúhelníku $APS$ v trojúhelníku $ABS$, viz následující obrázek.
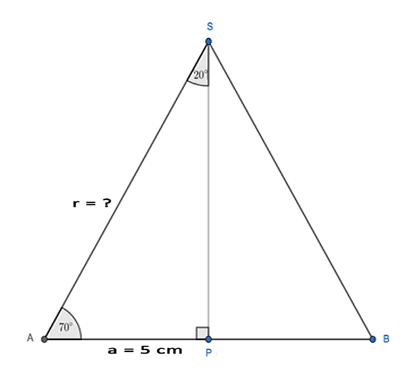
Délka strany $AB$ je dána $$ a = \abs{AB} = 5 \, \text{cm} $$ Bod $P$ je patou kolmice na stranu $AB$ spuštěné z bodu $S$ rovnoramenného trojúhelníku $ABS$ a leží tedy ve středu úsečky $AB$ $$ \abs{AP} = \dfrac{1}{2} \abs{AB} = \dfrac{5}{2} \, \text{cm} $$ Velikost úhlu $ASP$ je rovna polovině úhlu $ASB$ $$ \abs{\uhel ASP} = \dfrac{1}{2} \abs{\uhel ASB} = \dfrac{1}{2} \cdot 40^\circ=20^\circ $$ Zbývající úhel při vrcholu $A$ je doplňkem úhlů $ASP$ $(20^\circ)$ a pravého úhlu $APS$ do přímého úhlu $(180^\circ)$ $$ \abs{\uhel SAP} = 180^\circ - 90^\circ - 20^\circ = 70^\circ $$
$\textbf{První způsob - pomocí funkce sinus}$
K výpočtu poloměru kružnice opsané $r$ využijeme pravoúhlého trojúhelníku $SAP$ a funkce sinus, která je definována jako poměr protilehlé odvěsny a přepony $$ \sin{20^\circ} = \dfrac{\abs{AP}}{r} \Rightarrow r=\frac{\abs{AP}}{\sin{20^\circ}} $$ A po dosazení vypočítáme velikost poloměru $r$ $$ r = \dfrac{\dfrac{5}{2}}{0,342020143} = 7,309511 \doteq \vysledek{7,3 \, \text{cm}} $$
$\textbf{Druhý způsob - pomocí funkce kosinus}$
K výpočtu poloměru kružnice opsané $r$ využijeme pravoúhlého trojúhelníku $SAP$ a funkce kosinus, která je definována jako poměr přilehlé odvěsny a přepony \begin{align*} \cos{70^\circ} &= \dfrac{\abs{AP}}{r} \qquad \text{z rovnice vyjádříme $r$}\\ \cos{70^\circ} &= \dfrac{\abs{AP}}{r} \qquad / \, \cdot \dfrac{r}{\cos{70^\circ}}\\ r &= \dfrac{\abs{AP}}{\cos{70^\circ}} \end{align*} Po dosazení vypočítáme velikost poloměru $r$ \begin{align*} r &= \dfrac{\abs{AP}}{\cos{70^\circ}} = \\ &= \dfrac{\dfrac{5}{2}}{0{,}342\,020} = \\ &= 7{,}309\,511 \doteq \\ &\doteq \vysledek{7,3 \, \text{cm}} \end{align*}
$ \textbf{Výsledek} $ $$ \vysledek{r \doteq 7,3 \, \text{cm}} $$
$ \textbf{Odpověď} $
Poloměr kružnice opsané $r \doteq 7,3 \, \text{cm}$.
$ \textbf{Konec příkladu} $
Štítky: funkce, goniometrické funkce, trigoniometrie, mnohoúhelníky, výpočty
Strana pravidelného devítiúhelníku je $a=5\,\text{cm}$. Vypočítejte poloměr kružnice, kterou lze danému devítiúhelníku opsat.
$ \textbf{Řešení} $
Poloměrem $r$ kružnice opsané pravidelnému devítiúhelníku ABCDEFGHI je délka ramene rovnoramenného trojúhelníku $ABS$, viz následující obrázek.

Velikost úhlu $ASB$ v pravidelném devítiúhelníku je rovna devítině plného úhlu ($360^\circ$) a vypočteme ji $$ \abs{\uhel ASB}=360^\circ : 9 = 40^\circ $$ Velikost poloměru $r$ vypočteme pomocí pravoúhlého trojúhelníku $APS$ v trojúhelníku $ABS$, viz následující obrázek.

Délka strany $AB$ je dána $$ a = \abs{AB} = 5 \, \text{cm} $$ Bod $P$ je patou kolmice na stranu $AB$ spuštěné z bodu $S$ rovnoramenného trojúhelníku $ABS$ a leží tedy ve středu úsečky $AB$ $$ \abs{AP} = \dfrac{1}{2} \abs{AB} = \dfrac{5}{2} \, \text{cm} $$ Velikost úhlu $ASP$ je rovna polovině úhlu $ASB$ $$ \abs{\uhel ASP} = \dfrac{1}{2} \abs{\uhel ASB} = \dfrac{1}{2} \cdot 40^\circ=20^\circ $$ Zbývající úhel při vrcholu $A$ je doplňkem úhlů $ASP$ $(20^\circ)$ a pravého úhlu $APS$ do přímého úhlu $(180^\circ)$ $$ \abs{\uhel SAP} = 180^\circ - 90^\circ - 20^\circ = 70^\circ $$
$\textbf{První způsob - pomocí funkce sinus}$
K výpočtu poloměru kružnice opsané $r$ využijeme pravoúhlého trojúhelníku $SAP$ a funkce sinus, která je definována jako poměr protilehlé odvěsny a přepony $$ \sin{20^\circ} = \dfrac{\abs{AP}}{r} \Rightarrow r=\frac{\abs{AP}}{\sin{20^\circ}} $$ A po dosazení vypočítáme velikost poloměru $r$ $$ r = \dfrac{\dfrac{5}{2}}{0,342020143} = 7,309511 \doteq \vysledek{7,3 \, \text{cm}} $$
$\textbf{Druhý způsob - pomocí funkce kosinus}$
K výpočtu poloměru kružnice opsané $r$ využijeme pravoúhlého trojúhelníku $SAP$ a funkce kosinus, která je definována jako poměr přilehlé odvěsny a přepony \begin{align*} \cos{70^\circ} &= \dfrac{\abs{AP}}{r} \qquad \text{z rovnice vyjádříme $r$}\\ \cos{70^\circ} &= \dfrac{\abs{AP}}{r} \qquad / \, \cdot \dfrac{r}{\cos{70^\circ}}\\ r &= \dfrac{\abs{AP}}{\cos{70^\circ}} \end{align*} Po dosazení vypočítáme velikost poloměru $r$ \begin{align*} r &= \dfrac{\abs{AP}}{\cos{70^\circ}} = \\ &= \dfrac{\dfrac{5}{2}}{0{,}342\,020} = \\ &= 7{,}309\,511 \doteq \\ &\doteq \vysledek{7,3 \, \text{cm}} \end{align*}
$ \textbf{Výsledek} $ $$ \vysledek{r \doteq 7,3 \, \text{cm}} $$
$ \textbf{Odpověď} $
Poloměr kružnice opsané $r \doteq 7,3 \, \text{cm}$.
$ \textbf{Konec příkladu} $